はじめに
今回は効果量で用いられるコーエンのd(Cohen’s d)をpythonで求めていきます。
コーエンのdとは?
コーエンのdとは2つのグループ間に違いがあるのか?ということを確認していくためのものです。 またコーエンのdとヘッジのg(Hedges’ g)と並び、効果量の中でも"d族"と呼ばれており、2グループ間の"差"を調べていくものです。 一方で"r族"と呼ばれる効果量があるのですが、これは"関係の強さ"を表す指標として知られています。
それではコーエンのdとはなにかをまず定義から見ていきます。 以下に定義を示します。

ここからわかるように2グループの平均の差って標準偏差と比べた時どのくらいの割合なん?ってことですね。 dの基準ですが、一般的に0.2だと小、0.5だと中、0.8だと大とされています。 またコーエンのdは分布の重なりと解釈をすることも可能です。 0.2だと重なりが82.7%、0.5だと重なりが67.0%、0.8だと重なりが52.6%となります。 重なっている部分が多いと、2つの分布に違いがそこまでないのは直感的にわかりますよね。 この重なりの概念を理解することができると同じ平均でも標準偏差が違うと効果量が変わることもすんなり理解できるかと思います。 以下のイメージ図を参考にしてください。(本来ならもっと重なりますが、あくまでイメージとして。)
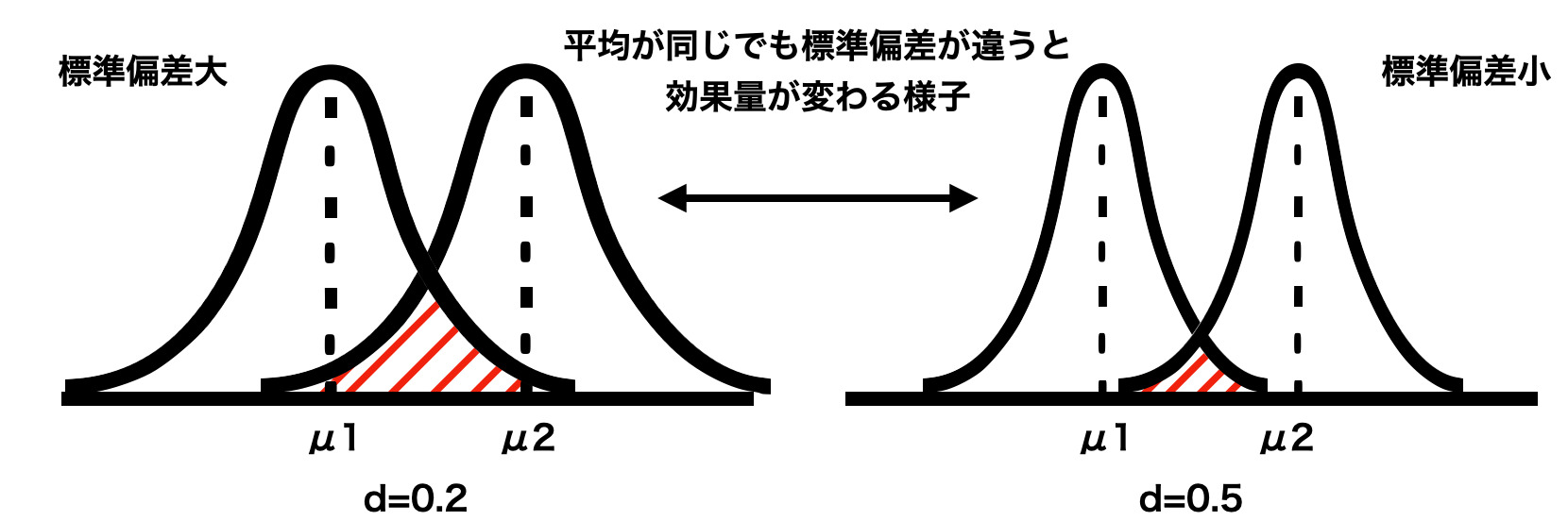
pythonでの計算方法
それではpythonでの計算方法についてみていきましょう。 まずグループ1(x1)とグループ2(x2)のデータを作成していきます。 今回は平均の差が10、標準偏差が10のものを用意します。
import numpy as np
mean_1 = 70
sigma_1 = 10
mean_2 = 80
sigma_2 = 10
x_1 = np.random.normal(mean_1, sigma_1, 10000)
x_2 = np.random.normal(mean_2, sigma_2, 10000)
作成したデータを描画してみましょう。
import matplotlib.pyplot as plt
plt.hist(x_1, bins=100, label='x1', alpha=0.5)
plt.hist(x_2, bins=100, label='x2', alpha=0.5)
plt.legend()
plt.show()
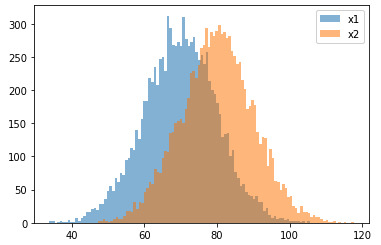
それではコーエンのdを求めていきます。
今回numpyを使って関数を実装していきます。
def cohens_d(x1, x2):
n1 = len(x1)
n2 = len(x2)
x1_mean = x1.mean()
x2_mean = x2.mean()
s1 = x1.std()
s2 = x2.std()
s = np.sqrt((n1*np.square(s1)+n2*np.square(s2))/(n1+n2))
d = np.abs(x1_mean-x2_mean)/s
return d
それではdを求めてみます。
print(cohens_d(x_1, x_2))
### 出力
# 1.0026758771680042
今回は平均値の差が10で、標準偏差が10なので1という出力は妥当だといえますね。