はじめに
距離というと2点間の距離を真っ先に思いつきますが、世の中にはさまざまな距離の定義が存在します。 ここではユークリッド距離、マンハッタン距離, チェビシェフ距離、ミンコフスキー距離について説明を行い、pythonでの実装方法を紹介します。
ユークリッド距離(Euclidean Distance)
これが真っ先に思いつく距離のことです。 2点間の距離の場合以下のように定義できます。 x=(x_0, x_1),y=(y_0, y_1)とすると
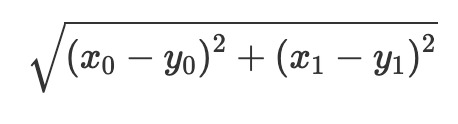
また多次元に拡張することも可能であり、その場合以下のように定義されます。
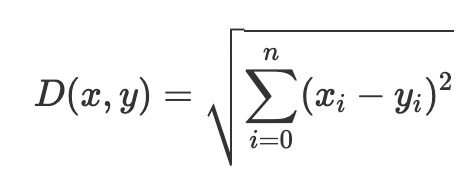
pythonでは以下のようになります。
>>> import numpy as np
>>>
>>> x = np.array([1, 1])
>>> y = np.array([2, 2])
>>>
>>> np.linalg.norm(x-y)
1.4142135623730951
しかしユークリッド距離は低次元の距離を測定する時はいいのですが、高次元を扱う際には不適らしいです。 そのため機械学習ではあまり使われないとか。 この辺はまた違う記事で書ければと思います。
マンハッタン距離(Manhattan Distance)
マンハッタン距離(もしくはL1距離)はユークリッド距離のように直線の距離を計算するのではなく、直角で動いたときの最短距離といえばいいでしょう。 つまり将棋でいえばユークリッド距離は角、マンハッタン距離は飛車です(?) 以下、イメージ図。
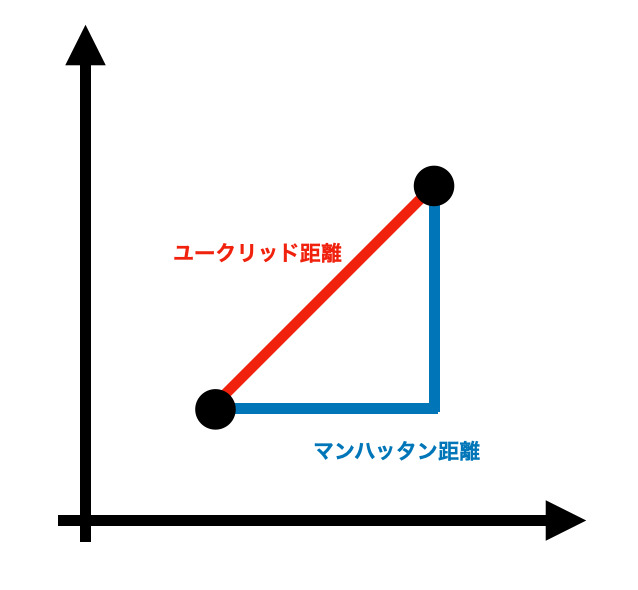
定義は以下の通り。
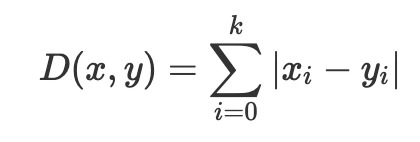
>>> import numpy as np
>>>
>>> a = np.array([1, 1])
>>> b = np.array([2, 2])
>>>
>>> np.linalg.norm(a - b, ord=1)
2.0
データセットに離散値が含まれる際に使うといいとか。 この距離は高次元でもうまくいきそうな感じだが、解釈性が困難になるので注意が必要である。
チェビシェフ距離(Chebyshev Distance)
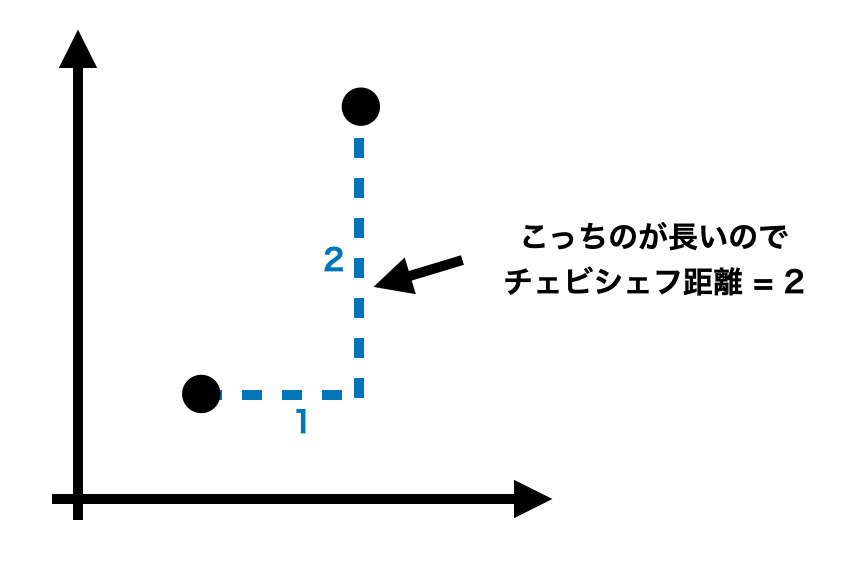
チェビシェフ距離は座標次元ごとで求めた差で一番大きいものを指します。 これもイメージ図をみた方がはやいでしょう。 この図の場合横軸の差は1, 縦軸の差は2となります。 この2つで大きい方は当然2なので、チェビシェフ距離は2となります。 簡単ですね。
定義は以下の通り。
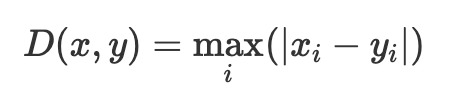
これもscipyにて実装されています。
>>> from scipy.spatial.distance import chebyshev
>>>
>>> a = np.array([1,1,1])
>>> b = np.array([1,2,4])
>>>
>>> chebyshev(a, b)
3
チェビシェフ距離に関してはいまいちどこで使えばいいのかわかってません(笑) 倉庫のロジスティクスやクレーンゲームで使われるみたいですが、ここはしっかり分かり次第また共有します。
ミンコフスキー距離(Minkowski Distance)
この距離はいままで紹介してきたものと比べると結構複雑です。 というか僕の認識では、ユークリッド距離、マンハッタン距離、チェビシェフ距離を一般化したようなものというイメージです。
定義は以下の通り。
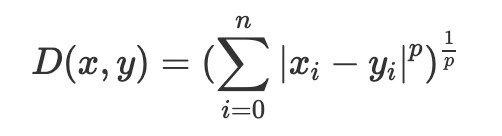
ここでいうpにおいて
- p=1にするとマンハッタン距離
- p=2にするとユークリッド距離
- p=∞にするとチェビシェフ距離
になることがわかるかなと思います。 pが小さい値だと差が小さい成分も考慮することができ、pが大きくなるにつれ小さい成分が無視されていきます。 マンハッタン距離の際は全ての差を足していったので小さい成分も考慮しており、チェビシェフ距離の時は差が最大の成分だけ使ってるのでなんとなくいっている意味もわかるかと思います。
scipyにて実装されています。
>>> from scipy.spatial.distance import minkowski
>>>
>>> a = np.array([1,1,1])
>>> b = np.array([1,2,4])
>>>
>>> minkowski(a, b, 1) #p=1
4.0
>>> minkowski(a, b, 2) #p=2
3.1622776601683795
ミンコフスキー距離を使う利点は最適なpを探索できることらしいですがいまいちよくわかっていません。