はじめに
今回はscipy.optimize.curve_fitを用いて色々な関数のカーブフィッティングをしていきます。
ライブラリ
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from sklearn.metrics import r2_score
1次関数
ダミーデータ
# 3x+5を真の関数としてノイズ付きのデータを準備
x = np.linspace(0, 1, 10)
a_t = 3
b_t = 5
y_t = a_t * x + b_t
y_noise = y_t + 0.25 * np.random.default_rng().normal(size=x.size)
plt.scatter(x, y_noise, color="black", label="data")
plt.plot(x, y_t, color="black", label=f"{a_t}x+{b_t}", linestyle="dotted")
plt.legend()
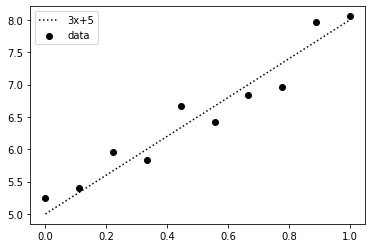
axでフィッティング
def proportion(x, a):
return a * x
# フィッティング
popt, pcov = curve_fit(proportion, x, y_noise)
y_pred = proportion(x, *popt)
r2 = r2_score(y_noise, y_pred)
# 可視化
plt.scatter(x, y_noise, color="black", label="data")
plt.plot(x, y_t, color="black", label=f"{a_t}x+{b_t}", linestyle="dotted")
plt.plot(x, y_pred, color="red", label=f"{np.round(popt[0], 2)}x")
plt.title(f"r2={r2}")
plt.legend()
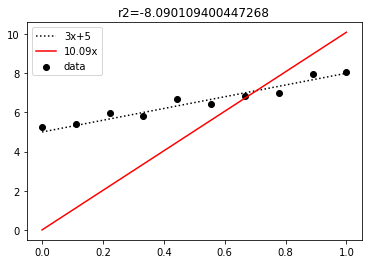
もちろんそこまでfitしない。
ax+bでフィッティング
def line(x, a, b):
return a * x + b
# フィッティング
popt, pcov = curve_fit(line, x, y_noise)
y_pred = line(x, *popt)
r2 = r2_score(y_noise, y_pred)
# 可視化
plt.scatter(x, y_noise, color="black", label="data")
plt.plot(x, y_t, color="black", label=f"{a_t}x+{b_t}", linestyle="dotted")
plt.plot(x, y_pred, color="red", label=f"{np.round(popt[0], 2)}x+{np.round(popt[1], 2)}")
plt.title(f"r2={r2}")
plt.legend()
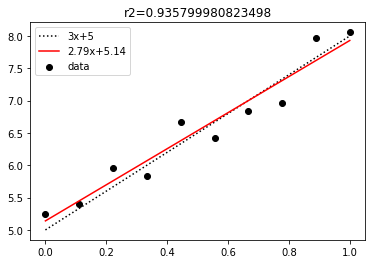
もちろんfit
2次関数
ダミーデータ
x = np.linspace(-1, 1, 20)
a_t = 10
b_t = 5
c_t = -30
y_t = a_t * np.square(x) + b_t * x + c_t
y_noise = y_t + 1.0 * np.random.default_rng().normal(size=x.size)
plt.scatter(x, y_noise, color="black", label="data")
plt.plot(x, y_t, color="black", label=f"{a_t}x^2+{b_t}x+{c_t}", linestyle="dotted")
plt.legend()
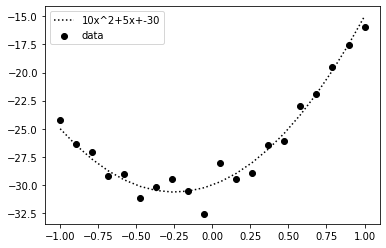
フィッティング
def quadratic(x, a, b, c):
return a * np.square(x) + b * x + c
# フィッティング
popt, pcov = curve_fit(quadratic, x, y_noise)
y_pred = quadratic(x, *popt)
r2 = r2_score(y_noise, y_pred)
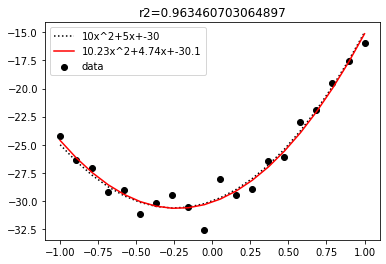
# 可視化
plt.scatter(x, y_noise, color="black", label="data")
plt.plot(x, y_t, color="black", label=f"{a_t}x^2+{b_t}x+{c_t}", linestyle="dotted")
plt.plot(x, y_pred, color="red", label=f"{np.round(popt[0], 2)}x^2+{np.round(popt[1], 2)}x+{np.round(popt[2], 2)}")
plt.title(f"r2={r2}")
plt.legend()
指数関数
ダミーデータ
x = np.linspace(-1, 1, 20)
a_t = 2
b_t = 4
c_t = 5
y_t = a_t * np.exp(-b_t * x) + c_t
y_noise = y_t + 5.0 * np.random.default_rng().normal(size=x.size)
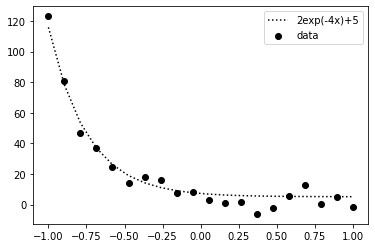
plt.plot(x, y_pred, color="black", label=f"{a_t}exp(-{b_t}x)+{c_t}", linestyle="dotted")
plt.scatter(x, y_noise, color="black", label="data")
plt.legend()
フィッティング
def func(x, a, b, c):
return a * np.exp(-b * x) + c
# フィッティング
popt, pcov = curve_fit(func, x, y_noise)
y_pred = func(x, *popt)
r2 = r2_score(y_noise, y_pred)
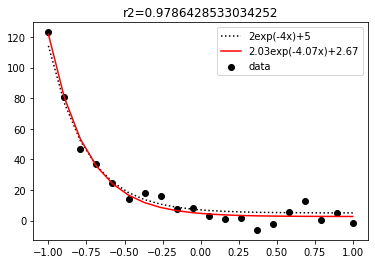
# 可視化
plt.scatter(x, y_noise, color="black", label="data")
plt.plot(x, y_t, color="black", label=f"{a_t}exp(-{b_t}x)+{c_t}", linestyle="dotted")
plt.plot(x, y_pred, color="red", label=f"{np.round(popt[0], 2)}exp(-{np.round(popt[1], 2)}x)+{np.round(popt[2], 2)}")
plt.title(f"r2={r2}")
plt.legend()
さいごに
フィッティングする時の関数設計は単調性・極限を意識することが大切。(記事に関係なし)