import numpy as np
import matplotlib.pyplot as plt 
from scipy.optimize import curve_fit
from sklearn.metrics import r2_score

# ダミーデータ
xx, yy = np.meshgrid(np.linspace(-10, 10, 10), np.linspace(-10, 10, 10))
grid_data = np.c_[xx.ravel(), yy.ravel()]

def func(data, a, b, c):
    return a*data[:,0] + b*data[:,1]**2 + c

a_t = -5
b_t = 2
c_t = 5
z_t = func(grid_data, a_t, b_t, c_t)
z_noise = z_t + 3 * np.random.default_rng().normal(size=z_t.size)

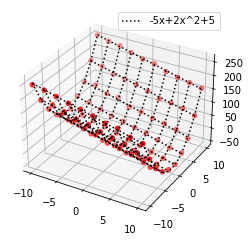
# 可視化
fig = plt.figure()
ax = fig.add_subplot( 1, 1, 1, projection='3d')
ax.scatter(grid_data[:,0], grid_data[:,1], z_noise, color="red")
ax.plot_wireframe(xx, yy, a_t*xx + b_t*yy**2 + c_t, color='black', linestyle='dotted', label=f"{a_t}x+{b_t}x^2+{c_t}")
plt.legend()
plt.show()

# フィッティング
popt, pcov = curve_fit(func, grid_data, z_noise)
z_pred = func(grid_data, *popt)
r2 = r2_score(z_noise, z_pred)

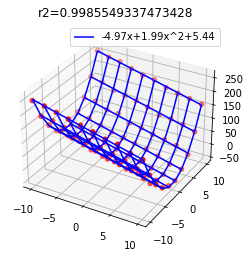
# 可視化
fig = plt.figure()
ax = fig.add_subplot( 1, 1, 1, projection='3d')
ax.scatter(grid_data[:,0], grid_data[:,1], z_noise, color="red")
ax.plot_wireframe(xx, yy, popt[0]*xx + popt[1]*yy**2 + popt[2], color='blue', label=f"{np.round(popt[0], 2)}x+{np.round(popt[1], 2)}x^2+{np.round(popt[2], 2)}")
plt.legend()
plt.title(f"r2={r2}")
plt.show()